こちらの記事で、概念の集合という考え方をご紹介しました。
以下では、概念の集合を応用した理論や方法論をご紹介します。
・・・
概念の集合の応用方法
ここでは、参照平面、概念空間、未概念法という3つの考え方をご紹介します。
・・・
応用方法①【概念の集合】から【参照平面】へ
参照平面とは、「概念の集合から構成された平面」を意味する概念です。
参照平面は、メタ的思考、多角的思考、認知バイアスの回避などを可能にする思考ツールです。
別の記事で詳しく解説させていただきますが、
参照平面では、概念は「光学的なレンズ」のような役割を果たすものと考えます。
光学レンズは、光を屈折させ、焦点を結び、像を浮かび上がらせます。
人間の思考プロセスにおいて、概念は、同様の機能を持っているのです。
【参照平面】とは言わば「光学的なレンズの集合体」であり、「無限に多様なレンズの集合体から構成された平面」である、というのが正確なイメージです。
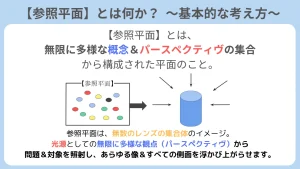
【参照平面】は、あらゆる「対象」や「問題」を、
光源としての無限に多様な異なる概念や観点(パースペクティヴ)から照射し、眺めることを主眼におく、光をモチーフとした概念です。
・・・
具体例を挙げてみたいと思います。
参照平面とは、概念の集合から構成された平面のことでした。
この参照平面では、例えば「分野別参照平面」という名称で、学問分野ごとに概念の集合を分類したうえで表示することができます。
すべての学問分野の概念群をごちゃ混ぜにして集合を作ることもできるし、分野ごとに整理して集合を作ることもできます。
以下は、分野ごとに整理してある概念の集合の事例です。
概念の集合の事例
哲学
(無知の知、存在/無、イデア、実体、魂、形相/質料、中庸、四原因、カテゴリー、コギト、方法的懐疑、神=自然、属性、様態、モナド、予定調和、充足理由率、理性、現象、物自体、精神、弁証法、実存、倫理、絶望、永遠回帰、超人、エポケー、アポリア、差異、反復、欲望機械、脱構築etc…)
数学
(集合、関数、定数、変数、方程式、直線、曲線、グラフ、傾き、次数、係数、最大値、最小値、実数、整数、素数、複素数、行列、ベクトル、線形変換、群、環、体、積分、微分、極限、連続性、導関数、偏微分、フーリエ変換、帰納法、無限大、無限小、位相空間、距離、コーシー列、収束、トポロジー、etc…)
論理学
(前提、帰結、推論、命題、真偽、肯定/否定、演算、真理値、論理式、帰納/演繹法、逆、裏、対偶、仮定、同値、包含、矛盾、誤謬、論理関数、量化子、命題変数etc…)
言語学
(音素、形態素、語幹、接辞、文法、構文、語彙、形態、語法、音声、音韻、語彙意味、構造、名詞句、動詞句、文の要素、統語関係、語順、言語機能、言語変異、e)
心理学
(意識、無意識、思考、感情、学習、記憶、古典的条件付け、オペラント条件付け、パーソナリティ、動機付け、人格、知能、自己効力感、発達段階、アイデンティティetc…)
認知科学
(知覚、注意、記憶、思考、言語、意思決定、学習、問題解決、スキーマ、認知バイアス、認知的不協和、認知発達、パターン認識、知識表現、認知モデル、認知処理etc…)
統計学
(平均、中央値、最頻値、分散、標準偏差、確率分布、正規分布、二項分布、ポアソン分布、信頼区間、仮説検定、p値、相関係数、回帰直線、標本、母集団、誤差、統計的有意性、標本調査、データの可視化、外れ値、モンテカルロ法、ブートストラップ法、時系列分析、因子分析、クラスター分析、主成分分析etc…)
経済学
(市場、需要、供給、DS曲線、均衡、価格、弾力性、限界効用、パレート効率、総需要、総供給、貯蓄率、限界生産性、国民所得、GDP、経済成長率、失業率、金融政策、財政政策、貨幣供給、利子率、政府支出、税収、公共投資、投資、貿易収支、為替レート、経済循環、景気変動、国際収支、経済政策、完全競争、外部性、公共財、機会費用、比較優位、景気循環、インフレーション、デフレーションetc…)
—————————————————
物理学
(速度、質量、加速度、ニュートンの運動法則、万有引力の法則、マクスウェル方程式、熱力学第二法則、シュレーディンガー方程式、プランク定数、エントロピー、電子スピン、光量子、量子トンネル効果、パウリの排他原理、ボーアモデル、ヒッグス機構、超対称性、不確定性原理、etc…)
化学
(原子軌道、モル濃度、化学平衡、電気陰性度、共有結合、イオン結合、酸化還元反応、酸・塩基、ファンデルワールス力、水素結合、化学反応速度、触媒、電解質、同位体、結晶構造、分子軌道理論、ギブス自由エネルギー、エントロピー、ハイブリッド軌道、放射年代測定etc…)
生物学
(細胞、遺伝子、DNA複製、RNA転写、タンパク質合成、細胞分裂、無性/有性生殖、ミトコンドリア、葉緑体、免疫反応、共進化、自然選択、適応、遺伝子プール、ホメオスタシス、進化、形態形成、個体群動態、相互作用、食物連鎖etc…)
生理学
(細胞、組織、臓器、系統、ホルモン、神経伝達、心拍数、呼吸、血圧、体温、代謝、エネルギー、酸素供給、栄養素、体液バランス、筋肉収縮、神経系、内分泌系、循環系、消化系、etc…)
神経科学
(ニューロン、グリア、神経伝達物質、シナプス、シナプス可塑性、受容体、活動電位、ドーパミン、セロトニン、グルタミン酸、GABA、ミエリン、大脳皮質、海馬、脳幹、皮質下核、視覚野、運動野、脳波etc…)
免疫学
(自然免疫、獲得免疫、抗原、抗体、免疫細胞、サイトカイン、補体、リンパ球、ナチュラルキラー細胞、B細胞、T細胞、マクロファージ、樹状細胞、自己免疫、免疫寛容、免疫応答、免疫記憶、抗原提示etc…)
遺伝子学
(DNA、RNA、遺伝子、コドン、発現、クロマチン、転写、翻訳、エピジェネティクス、ミューテーション(突然変異)、遺伝子多型、遺伝暗号、染色体、遺伝子組み換え、遺伝子編集、遺伝子型etc…)
天文学
(ケプラーの法則、太陽系外惑星、恒星進化、ホワイトドワーフ、赤色巨星、超新星、惑星、銀河、銀河団、クェーサー、ブラックホール、ブラックホール、ダークマター、ビッグバン理論ビッグバン、膨張宇宙、暗黒物質、太陽風、ハッブル定数、宇宙の加速膨張、宇宙マイクロ波背景放射、重力レンズ効果、オーロラetc…)
少し長くなってしまいましたが、このように学問別の多様な概念の集合を考えることで
一つの問題に対して、様々な観点(パースペクティヴ)から問題にアプローチできることがわかります。
先ほどの光のアナロジーを思い出してみて下さい。
参照平面とは、光源としての無限に多様な観点&概念の集合から光を照射し、
対象のあらゆる像を浮かび上がらせます。
問題解決シーンにおいては、問題を無限に多様な概念の集合を用いて思索し、
無限に多様な観点から眺め、解釈することを可能にするのです。
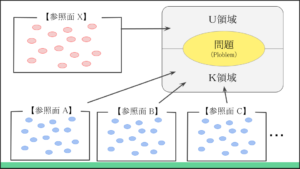
さらに、参照平面は、定義に「平面」を含んでいます。
これは、無数の情報を視覚的にパネル表示することもできることを意味します。
参照平面は、概念の集合を他者と共有できる機能をもつ思考ツールです。
この分野的参照平面は、例えば、現代社会における複雑な問題や、分野横断的な考え方をしなければ解決できない問題について取り組むとき、効果を発揮します。
これは超学際(トランスディシプリナリティー)的な考え方をするうえで極めて重要です。
・・・
応用方法②【概念の集合】から【概念空間】へ
概念の集合は、そのまま概念空間として考えることができます。
概念空間については、次の幾つかの記事で解説しているので、ぜひご覧下さい。
概念の集合という考え方を応用すると、あらゆる問題を解決するうえで役立つ非常に強力な理論&方法論(アプローチ)を構築することができます。
この考え方を問題解決のために理論化・体系化したのが、【概念空間論】です。
・・・
応用方法③【概念の集合】から【未概念法】へ
問題解決のシーンでは、新しい概念(未知の概念)を創造することがとても重要です。
未概念法は、新しい概念を連続的に創造することを可能にする方法論です。
以下は、未概念の典型的な事例です。
※他にも方法が色々あります。
未概念の事例
α量、β性、γ化、δ系,ε度,ζ法,η的,θ層,ι分類,κ構造,λ順序,μ関係,ν領域,ξ部分,ο過程,π前提,ρ分類,σ条件,τ状況,υ接続,φ配分,χ分割.
こうした未知の概念の材料を用いて、短期間に大量の新しい概念を創造していきます。
これによって、問題が解決できない最大の原因である概念の不足状態を解消することができます。
未概念法は、あらゆる問題が解決に至る可能性を近似的に極限まで引き上げることができる新しい思考法です。
※詳細はこちら(概要)
・・・
このように、概念の集合という考え方は、非常に幅広い応用の可能性が考えられます。



コメント