いかなる問題も、それが発生したのと同じ次元で解決することはできない。
(We cannot solve our problems with the same thinking we used when we created them.)
――アルベルト・アインシュタイン
こんにちは、馬渕です。
このページでは、概念空間論の枠組みで使うことができる、「考え方の集合」を考えるという思考法をご紹介します。
この思考方法は、非常に汎用性が高く、あらゆる分野で活用することができ、また様々な問題解決シーンにおいて高い効果を発揮します。
あなたがどの分野に携わる方でも、きっとお役に立つと思うので、最後までお読み頂けたら嬉しいです。
・・・
動画解説
・・・
参照平面とは?
今回ご紹介する思考方法では、【参照平面】という概念を用います。
※【参照平面】の詳細については、こちらをご覧ください。

【参照平面】は、概念の集合から構成される平面のことなのですが、主に4つの重要な機能があります。
—————————————
第1の機能:概念の集合を自由に分類・グループ化できる
第2の機能:概念の集合に解釈を加え「〇〇の集合」を作れる
第3の機能:概念の集合を既知のグループと未知のグループに分ける
第4の機能:概念の集合を平面上に表示しかつ共有できる
—————————————
第1の機能として、自由に任意の概念の集合を作ることができる機能を持ちます。
第2の機能として、概念の集合に新しい解釈を加えて、
「概念の集合=〇〇の集合」というように、新しい集合を作ることができます。
今回は、概念の集合を考え方の集合として解釈して使用していきます。
・・・
「考え方の集合」を使用する3つの手順
今回は、3つのステップに分けて考えていきたいと思います。
——————————-
ステップ①「考え方の集合」を考える
ステップ②「既知の考え方/未知の考え方」を分類する
ステップ③「既知の考え方」を疑い、「新しい考え方」へ遷移する
——————————-
・・・
ステップ①「考え方の集合」を考える
参照平面とは、概念の集合から構成される平面のことでした。
自由に、任意の概念の集合を考えることができます。
さらに、概念の集合に解釈を加え、考え方の集合として扱います。
抽象化してモデル化してみると、次のような「考え方の集合」を考えることができます。
【考え方の集合】={考え方1,考え方2,考え方3,‥‥‥考え方n}
※以下は、考え方の集合の事例またはイメージ図です。
考え方の集合の事例
問題、問い、解、メタ、抽象、具体、前提、帰結、根拠、結論、場合、条件、分岐、パターン、観点、焦点、像、定義、分類、包摂、配置、分離、接続、分割、統合、全体、部分、構造、体系、要素、集合、順序、推移、変化、過程、変換、置換、識別、判断、評価、決定、解釈、認識、自覚、懐疑、明晰、不明瞭、明確、曖昧、十全、比較、対照、類推、推論(帰納、演繹など)、量的(単数、複数など)、質的、関係性(同等、類似、相違)、可能性(必然、偶然、蓋然)、仮定、仮説、理論、証明、論証、問題解決(現状、目標、計画、設計、戦略)、曲線、収束、発散etc…
これらの概念のリストは、考え方の集合としても扱えそうですよね。
もちろん様々な学問分野の概念の集合を考えると、それも「考え方の集合」として解釈することができるでしょう。
考え方の集合の事例
哲学的な考え方
(実在論、倫理学、唯物論、現象学、実存主義、形而上学、認識論、功利主義、相対主義、規範倫理)
数学的な考え方
(集合、位相、代数、微積分、数論、確率、統計、線形代数、数理論理学、幾何学)
論理学的な考え方
(演繹、帰納、推論、命題、矛盾、対偶、排中律、三段論法、論理式、同値)
心理学的な考え方
(無意識、行動主義、認知行動療法、自己効力感、パーソナリティ、感情知能、発達心理学、社会心理学、動機づけ、トラウマ)
認知科学的な考え方
(情報処理モデル、メンタルモデル、認知地図、パターン認識、デュアルプロセス理論、ワーキングメモリ、概念形成、知覚、学習理論、言語理解)
神経科学的な考え方
(ニューロン、神経可塑性、シナプス、脳波、神経伝達物質、大脳皮質、海馬、前頭前野、ドーパミン、神経回路)
医学的な考え方
(疫学、病理学、予防医学、診断、治療、遺伝医学、感染症、外科、内科、リハビリテーション)
政治的な考え方
(リベラリズム、保守主義、権威主義、民主主義、ナショナリズム、社会主義、共和主義、君主制、全体主義、アナキズム)
物理学的な考え方
(力学、量子力学、相対性理論、熱力学、電磁気学、素粒子物理学、流体力学、光学、音響学、物質科学)
生物学的な考え方
(進化、遺伝子、細胞分裂、免疫系、生態系、自然選択、遺伝子発現、タンパク質合成、代謝、シグナル伝達)
統計学的な考え方
(標本、確率分布、回帰分析、仮説検定、偏差、相関、分散分析、モンテカルロ法、ベイズ推定、信頼区間)
経済学的な考え方
(需要/供給、市場均衡、インフレーション、効用、国民所得、比較優位、機会費用、限界効用、外部性、貿易)
社会学的な考え方
(社会構造、社会階級、再生産、文化資本、役割理論、コミュニティ、社会運動、ジェンダー、階層化、都市化、社会化)
人口学的な考え方
(出生率、死亡率、識字率、人口ピラミッド、移民、老齢化、人口分布、家族構造、人口爆発、出生率低下、都市化、世帯構成)
財政学的な考え方
(公共財、税収、政府支出、財政赤字、国債、累進課税、補助金、財政政策、税制改革、社会保障)

・・・
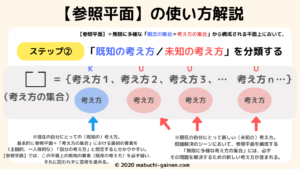
ステップ②「既知の考え方/未知の考え方」を分類する
【参照平面】には、第3の機能として、
概念の集合を既知のグループと未知のグループに区分する、という働きがあります。
この第3の機能を用いると、これまでに構成した「考え方の集合」を、
さらに既知の考え方のグループと未知の考え方のグループに分類することができます。
つまり、既存の古い考え方のグループ、新しい考え方のグループに分けるのですね。
特に後者の「未知の考え方」のなかに、当該の問題を解決するうえで必要な最適な考え方が含まれています。
・・・
ステップ③「既存の考え方」から「新しい考え方」へ
このように「考え方の集合」を準備できたら、参照平面を眺めながら、
「既存の考え方」に囚われずに、次々と未知の考え方に遷移(シフト)していく
ということを考えます。
概念空間論では、基本的に、人間の思い込みや信念、認知バイアスなどを前提として思考していきます。
この思い込みや信念は、我々が直面する問題の解決を妨げる最大の障害ですよね。
参照平面を通じて、考え方の集合というシステムを使えば、必ず何らかの思い込みを含んでいる、「現在の自分の考え方」を疑うことが原理的に保証されます。
これは、現代において数百もの種類が知られている、認知バイアス(思い込み)を回避するために私が社会に広めたい解決策の一つです。

この集合上の要素を次々と移行するとき、最大のポイントになるのが、問い(質問)を立てることです。
人間の思考は「問い」によって導かれ、その内容や方向性が決定されるからです。
そのため、「考え方の集合」のなかで次々と新しい要素=考え方に移行するため、こんな風に質問を投げ掛けます。
質問①現在の自分の考え方には、どんな思い込みがあるだろうか?
質問②自分にとっての未知の考え方(新しい考え方)とは何だろうか?
・・・
問題解決の絶対ルール
少し補足になるのですが、実践上で大事なポイントに触れておきたいと思います。
問題解決には、次のような重要なルールがあります。
問題を解決するためには、(当の問題に対して)適切な考え方を選択しなければならない。
このルールは、メタ的な思考法を使いこなすために必要になるものです。
【考え方の集合】={考え方1,考え方2,考え方3,‥‥‥考え方n}
こうした考え方の集合を構成する「未知の考え方」(新しい考え方)のなかには、あなたが直面している問題を解決するための適切な考え方が含まれています。
ということは、私たちが考えるべきことは、やはり「現在の自分の考え方」に囚われずに「新しい考え方」を意識することであり、
この「考え方の集合」を構成する様々な個々の要素を、次々と遷移(シフト)することなのですね。
・・・
「考え方の集合」を考えるメリット
「考え方の集合」という考え方には、非常に様々なメリットが得られます。
メリット①メタ的な思考が可能になり、問題解決力が高まる
「考え方の集合」を考えることによって、問題解決の力を高める効果が期待できます。
というのも、前述の通り、この「考え方の集合」というシステム内では、
「現在の自分の考え方」に固執せずに、次々と新しい考え方に移行(遷移)していくことを前提としているからです。
問題解決の可能性を高めるためには、
思い込みを疑うこと(メリット②)
新しい考え方を意識すること(メリット③)
この2つの点がとても重要になります。
メリット②既知の考え方(自分の考え方など)を疑うことができる
問題解決において、思い込みを疑うことは極めて重要だと言えます。
なぜなら、私たちが問題解決に取り組むとき、もし思い込みを完全に排することができていれば、問題を解決できている可能性が高いからです。
思い込みは、面白くもあり厄介でもある「意識することができない」という特徴を持っています。
ところが、「考え方の集合」を考えることによって、自分の考え方は相対化され、思い込みを疑うことが原理的に保証されるのです。
この考え方は、認知バイアス(思い込み)を回避するうえでも極めて有効です。
メリット③未知の考え方(新しい考え方)を意識できる
この「考え方の集合」では、必ず自分にとっての未知の考え方(新しい考え方)があることを想定します。
そのため、システム的に新しい考え方を創造することに意識が向きことが保証されます。
問題を解決できるのは、既存の古い考え方ではなく、自分にとっての新しい考え方です。
だからこそ、常に新しい考え方を含む「考え方の集合」を概念としてもっておくことが重要になります。
・・・
未知の考え方(新しい考え方)を生み出す方法論
この記事でお伝えしてきた「考え方の集合」という思考方法は、実はまだこれで終わりではありません。
最後に、一番大きな難問が残っています。
それは、問題解決シーンにおいて、
「考え方の集合」を構成する要素のなかで、どのようにして当の問題を解決するために必要な適切な未知の考え方(新しい考え方)を導き出すか?
というものです。
これは難問中の難問です。
というのも、もし、あらゆる問題に対して有効なこんな方法が存在したら、地球上のあらゆる問題が解決するわけで、勿論基本的には不可能だからです。
しかし、こうした問題解決のための新しい考え方(未知の考え方)を狙い通りに生み出すことは、近似的には可能で、
そのための方法が、【未概念法】という考え方です。
【未概念法】は、あらゆる問題の解決のために、より自由に(近似的に)新しい考え方を創造することができる方法論です。
【未概念法】は、非常に強力な考え方ですが、使いこなすのがかなり難しいです。
ただ、もしこの方法論の感覚を掴むことができれば、問題解決のための思考力を極限まで引き上げることができます。
メタ思考
「考え方の集合」は、かなり抽象度が高い、メタ的な思考方法です。
様々な問題解決のシーンのなかで「考え方の集合」を想定して、
既存の考え方に囚われずに思考を進め、新しい考え方を生み出すことができれば、
とても強力な武器になります。
そして参照平面という概念を用いると、メタ思考を促進することができるのです。
例えば、学生が何かの科目の勉強をするときも、
企業が抱えている課題を解消するために会議をするときも、
私たちが自分の人生について考えるときも、この思考方法を使うことが可能です。
最後に
この方法については、また別のところでもお話したいと思います。
※補足;数学ほど、厳密に「集合」を考える訳ではないので、集合論の教科書などで登場するような「集まり」として解釈してもらえたらと思います。
この思考方法によって、思い込みを疑うこと/未知の考え方に意識を向けること/メタ的に思考できること等が原理的に確保されるからです。



コメント