■■【未概念法】■■■
■未概念法の定義
未概念法とは、未概念という特殊な概念群を用い、新しい概念を連続的に創造する方法論である。
未概念法では、概念の不足状態を解消することができ、、問題解決の可能性を限りなく高めることができる。
以下では、前半において未概念法の原理を、後半でその原理に基づく手順を示すことにしたい。
未概念法の原理と方法
未概念法の原理および方法として、主に以下の3つの考え方が重要である。
—————————————————————–
1.未概念
2.思考の枠組み(※思考モデル、無限に多様なもの)
3.遷移度/明瞭度の機構
—————————————————————–
■1.未概念
未概念とは、つねに過渡的な生成状態にあるものと把握される変容性の概念のことである。
この言葉には、少なくとも次のような二つの意味が重ね合わせられている。
—————————————————————–
①未然性:未だ完成していない状態の概念
②未知性:未知の新しい概念
—————————————————————–
未概念は、未然性と未知性という二つの性質を備えている。
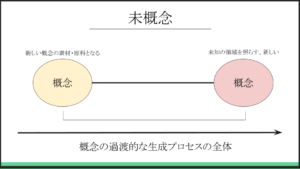
未然性とは、未だ概念の製作・創造プロセスが完了していない状態を意味する。
さらに、未然性とは、新しい未知の概念の原料や素材となる性質を指す。
未知性とは、未だ知られていない新しい状態を意味する。
また、未知性とは、概念が未知の領域に属することを指している。
この両性質は、未概念において同時に成立するため、統合された形で理解されなければならない。
未然性と未知性の組み合わせは、時間軸上でいえば、過去・現在・未来のすべてを包括することができる。
要するに、未概念とは、過渡的な生成状態にある概念の変容過程全体を包括的に表現するための用語なのである。
未概念法では、あらゆる概念を、つねに過渡的な生成状態にある変容性のものと見做す。
裏返せば、未概念法では、あらゆる概念を未概念化し、決して(完全には)安定化あるいは固定化せずに思考するのである。
■未概念化
未概念化とは、概念をつねに過渡的な生成状態にある変容性のものにすることである。
未概念法では、無限に多様な概念の集合Gは、未概念化される。
■未概念のイメージ
未概念の最も分かりやすい事例を挙げよう。
未概念=文字/記号+◯◯
{α量、β性、γ化、δ系,ε度,ζ法,η的,θ層,ι分類,κ構造,λ順序,μ関係,ν領域,ξ部分,ο過程,π前提,ρ分類,σ条件,τ状況,υ接続,φ配分,χ分割…}
■2.思考の枠組み(思考モデル)
定義:思考の枠組みとは、複数の概念同士の結び付きや組み合わせによって構築されるものである。
枠組みは、複数の概念の組み合わせによってできる、(抽象性において)最も高度な形成物である。
以下では、こうした枠組みを、分かりやすさのために思考モデルと呼ぶ。
構成パターン➡①自然発生的な生成、②あるいは自覚的な構築
枠組み化
枠組み化とは、複数の概念同士が組み合わさることで、ある程度の静止性や安定性をもつことである。
複数の概念の組み合わせは、もともと未概念からできた新しい概念同士の結び付きによって形成されたものでも、若干の安定性や固定性を持つことになる。
思考モデルの形成/構築
未概念法では、未概念化の考え方によって、新しい概念を連続的に創造する。
概念の量が増えると、複数の概念同士の結び付き・組み合わせが生じる
思考上の問題解決のプロセスでは、思考モデルが不可欠である。
後述の通り、未概念法では、無限に多様な思考モデルの集合を通じて思考する。
■未概念と思考の枠組み化(思考モデル)
未概念と枠組み(思考モデル)の間には、対照性と相互性という二つの関係性がある。
これらの関係性は、未概念法における2種類の思考や概念の運動の方向性を表している。
未概念とは、つねに過渡的な生成状態にあるものと把握される変容性の概念であり、
枠組み(思考モデル)とは、複数の概念の組み合わせによって生じるものであった。
—————————————————————–
①対照性
②相互性(反転性/浸透性)
—————————————————————–
対照性とは、一方では概念が未概念化によって溶解し、もう一方では枠組み化によって結晶化する、という正反対の状態や運動のことである。
相互性とは、概念が未概念化と枠組み化という対照性を示しながら、同時にそれぞれがもう一方の性質へ反転する状態や運動のことである。
両者には、次のような対照的な属性を表現する概念のグループを付与することができる。
—————————————————————–
未概念 :変容性、流動性、発散的、破壊的、解体的、混沌的、開放性、逸脱的、断片化…
枠組み :安定性、固定性、収束的、構築的、統合的、秩序的、閉鎖性、規律的、体系化…
—————————————————————–
しかし、これらの属性のグループは、未概念と枠組みに、固定的に配分されるものではない。
未概念と枠組みは、相互的な反転性をもつのである。
未概念は、未知の概念の創造の原料として使用されるが、同時に新しい枠組み(思考モデル)の構築へと向かう。
そのため、あらゆる瞬間において、安定化・固定化・収束化…という運動が起こる。
思考モデルは、複数の概念同士の結合によって構築されるが、同時にそのすべての構成要素はつねに未概念化される。
そのため、全体またはあらゆる部分に渡って、変容性、流動性、発散性…という運動が起こる。
未概念法のプロセスでは、無限に多様な概念の集合が用いられる。
無限に多様な概念の集合は、
すべてが未概念と見做され、新たな思考モデルの構築に寄与し、
新しい思考モデルの構成要素は、すべて溶解し未概念と化す。
未概念法において、無限に多様な概念の集合は、凄まじい速度で対照的かつ相互的な絶えざる運動を引き起こすのである。
生成と消滅、誕生と死、溶解と析出、融解と凝固、分離と統合、出現と消失、発展と衰退、拡張と収縮、統合と分裂、分散と集中、開放と閉鎖、破壊と創造、形成と解体、
■遷移度/明瞭度の機構
未概念法でも、遷移度/明瞭度の原理は重要な役割を果たす。
未概念法では、未概念を散布することで概念量を増大させ、遷移度/明瞭度の機構を駆動するのである。
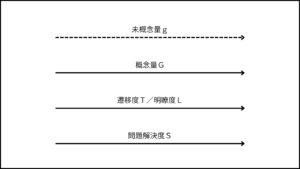
未概念(化)は、遷移度および明瞭度の機構を駆動する。
枠組み(化)は、遷移度と明瞭度の機構の稼働の効率性を上げ、威力やスピードをさらに高める。
■未概念法の手順
■未概念法の手順
次に、未概念法の大まかな手順、実践的なフローを概説したい。
—————————————————————–
①未概念群の散布
②新しい概念の創造(結晶化)
③新しい思考モデル(枠組み構築)
④新しい認識の獲得=遷移度/明瞭度の高まり
⑤問題解決
—————————————————————–
手順②,④,⑤は、遷移度/明瞭度の機構を構成する
三本の線分の順序及び組み合わせと重なるものである。
したがって、ここでは手順①と③が新たに加えられたことになる。
—————————————————————–
①未概念群の散布
第一の手順は、未概念群の散布である。

●地理学的モデル
解釈①未概念化は、K領域とU領域の間を架橋する。
遷移系:既知の概念は、未概念化によって変容性のものとなり、未知の概念の原料となり、U領域に流れ込む。
冒険系:
●光学的モデル
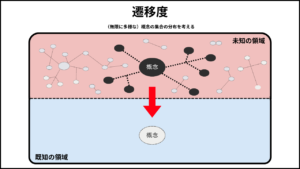
未知の領域は明瞭度が低い暗がりの状態にある範囲である。未知の領域が未知であるのは、概念が不足していることによる。そのため、まず未概念を散布する。
②新しい概念の創造
第二の手順として、次のステップでは、未知の領域に散布された未概念群をもとに、新しい概念を創造する。
③新しい思考モデル(枠組み構築)
第三の手順は、新しい思考モデル(枠組み)を構築することである。
大量の概念が手元に揃うと、自然に新しい思考の枠組みができあがってくる。
あるいは、自覚的に新しい思考の枠組みを構築する。
④新しい認識の獲得=遷移度、明瞭度の高まり、
第四の手順は、新しい認識を獲得することである。
これまでに創造した大量の概念、および構築した思考モデルを手掛かりとしながら、新しい洞察を獲得する。
●地理学的モデル
遷移モデル:新しい認識は、U領域からK領域に遷移する。
冒険モデル:新しい認識は、発見される。
●光学的モデル
この新しい認識は、未知の領域を照らし、明瞭度を高めるものである。
※⑤問題解決
第5の手順は、問題を解決することである。①~④の過程の帰結として、問題は解決に至る。
—————————————————————–
枠組み化・思考モデルの集合
未概念法では、無限に多様な思考モデルの集合を通じて思考/問題解決のプロセスをすすめる。
目的:遷移度/明瞭度を際限なく高めるため
構成要素:各々の思考モデルは、以下の要素を含む
—————————————————————–
①概念の集合:思考の枠組みを構成するもの
②包摂的な集合:問題の答えや解決方法を包摂する集合
③仮説的な概念:条件の集合、前提、仮定、方向性
④懐疑的な概念:思い込み、バイアスの集合
⑤創造的な概念:新しい未知の考え方、アプローチなど
—————————————————————–
—————————————————————–
①概念の集合:思考の枠組みを構成するもの
第一の要素は、概念の集合である。思考の枠組みを構成するものである。
顕在的には有限のものだが、潜在的には無限に多様なものといってよい。
②包摂的な集合:問題の答えや解決方法を包摂する集合
第二の要素は、解-包摂的な集合である。
③仮説的な条件集合:前提、仮定、方向性
第三の要素は、仮説的な条件である。
④懐疑的な集合:思い込み、バイアスの集合
第四の要素は、懐疑的な集合である。
⑤創造的な概念の集合:
第5の要素は、創造的な集合である。未知の要素や方法を含む
—————————————————————–
※補足;集合論的な把捉
上記の①~⑤をすべて集合論的な把捉によって考える。
◆無限に多様な思考モデルの集合
未概念法では、無限に多様な思考モデルの集合M(G)を想定して問題解決を図る。
理由:遷移度/明瞭度を高めること
思考モデル集合Mを考えるのは、遷移度/明瞭度を際限なく高めるためである。
※思考モデルの意義、未概念法において
未概念法による思考プロセスにおいて、「一つの思考モデル」のみを用いて問題解決を図ることはない。
未概念法の目標は、一つの思考モデルに留まること/その正しさを証明することではない
※この意味で、科学的な思考でも数学的な思考とも一致しない。
問題の完全な解決は、際限のない遷移度と明瞭度の高まりの果てにあるもの。
————————————————–
地理学的な状態:完全に未踏の到達地点
光学的な状態:完全な光に包まれる状態
————————————————–
複数の思考モデル間の遷移(パラダイム・シフト)に必要なもの
未概念法では、複数の思考モデル間を遷移(シフト)しながら思考を進め、問題解決を図る。
連続的なパラダイム・シフトの過程で、遷移度と明瞭度を際限なく高める続けるのである。
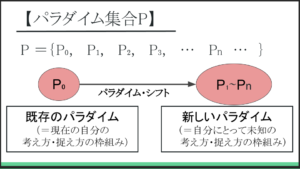
パラダイム・シフトの3つの条件は、未概念化と①~⑤(特に④と⑤)の要素によって、すべて満たされる。
————————————————–
④懐疑的な概念:思い込み、バイアスの集合
⑤創造的な概念:完全に未知の考え方、アプローチ
————————————————–



コメント