遷移度／明瞭度について

 

 

 

遷移度／明瞭度について

 

概念空間論における思考の自由さとは、思考の可能性すべてを実現しうることであり、思考の運動に焦点をあてた指標を表現するものである。しかし同時に、思考の自由さとは、認識の変容を自覚的に引き起こすことでもある。

そして認識の変容とは、遷移度／明瞭度の変化にほかならない。この意味において、概念空間論のすべては、遷移度／明瞭度を際限なく高めるために設計された体系的な枠組みである。

 

以下では、遷移度と明瞭度という概念について、次の順番でポイントを確認していく。

—————————————————————

１．遷移度と明瞭度の定義やイメージ

２．遷移度と概念の集合の関係

３．明瞭度と概念の集合の関係

３．遷移度と明瞭度の機構――①概念の集合、②遷移度と明瞭度、③問題解決の関係性

—————————————————————

 

第一に、遷移度という概念の基本的な定義、イメージ、事例、概念の集合の関係について。

第二に、明瞭度という概念の基本的な定義、イメージ、事例、概念の集合の関係について。

第三に、遷移度と明瞭度の機構について。

 

本節の最終的な目標は、この遷移度と明瞭度の機構（システム）を提示することである。

ここで遷移度と明瞭度の機構と呼んでいるのは、

またこの二つの概念は、相互的に影響を及ぼしあう関係性を持っている。

 

 

遷移度の概要

遷移度とは、認識領域に含まれる様々な要素の分布や配分状態を把握／表現するための概念である。

 

※最も典型的なものとして、概念の集合の分布や配分状態を考える。

※ただし、概念の集合だけでなく、認識や認識の様々な構成要素の遷移を考えることも多い。

 

そのため、まずはこのように定義できる。

 

遷移度とは、認識領域における概念の集合の分布や配分状態を把握／表現するための概念である。

 

以下では、概念の集合を中心として、この概念の詳細を確認しよう。

 

認識領域における概念の集合の分布とその変化を考えるために、次の４つのパターンを区別するのがよいだろう。

—————————————————————

①無遷移

②低遷移

③高遷移

④全遷移

—————————————————————

 

 

—————————————————————

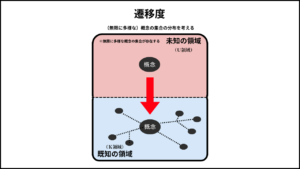
①無遷移

第一のパターンは、無遷移の状態である。

無遷移とは、未知の領域（Ｕ領域）から既知の領域（Ｋ領域）へ、概念の集合がまったく移行していない状態である。無遷移の状態では、未知の領域（Ｕ領域）に、有限の概念の集合の場合、あるいは無限に多様な概念の集合がすべて属している。反対に、既知の領域（Ｋ領域）には、いかなる概念も属していない。それゆえ、無遷移の状態にあるＫ領域は、白紙状態（タブラ・ラサ）と呼べるだろう。

認識主体の立場からすれば、手元に揃っていない状態である。

 

②低遷移

第二のパターンは、低遷移の状態である。

低遷移とは、未知の領域（Ｕ領域）から既知の領域（Ｋ領域）へ、まだ概念の集合の多くの部分が移行していない状態である。

 

③高遷移

第三のパターンは、高遷移の状態である。

高遷移とは、未知の領域（Ｕ領域）から既知の領域（Ｋ領域）へ、概念の集合の多くの部分が移行している状態である。

 

④全遷移

第四のパターンは、全遷移の状態である。

全遷移とは、未知の領域（Ｕ領域）から既知の領域（Ｋ領域）へ、概念の集合がすべて移行している状態である。

—————————————————————

 

注意点；低遷移／高遷移という表現

低遷移／高遷移という表現は、相対的な意味で使えるものに過ぎない。

高遷移は、低遷移の状態に比べれば遷移度が上であるが、全遷移の状態と比較すれば遷移度は低いといえる。

低遷移は、高遷移の状態に比べれば遷移度が低いが、無遷移の状態と比較すればわずかに遷移度は高いと言える。

 

有限の概念の集合／無限に多様な概念の集合

概念の集合は、有限のもの／無限に多様なものに分けられる。

上記の遷移度の区分については、概念の集合が、有限のものかあるいは無限に多様なものと考えるかによって、解釈や扱い方を変えなければならない。

—————————————————————

①無遷移

第一のパターンである無遷移の状態は、有限の概念の集合でも、無限に多様な概念の集合でも、大きく解釈を変える必要はない。

 

②低遷移／高遷移

低遷移／高遷移という表現は、有限の概念の集合を考える場合は、「少ない部分」「多くの部分」が遷移していると言っても差し支えないため、特に問題なく使用できる。

ただし、無限に多様な概念の集合を考える場合には、注意が必要である。

この場合は、未知の領域については無限に多様なものを想定しつつ、既知の領域の概念の集合については特定の目的や目標と照らして程度を判断するのがよいだろう。

というのは、このケースでは、未知の領域から既知の領域へどれほどの概念の集合が遷移していくとしても、未知の領域に膨大なものが留まり続ける。その大きさの程度も決定することができず、既知の領域に遷移したものの純粋な多寡を考えることはできないからである。

それゆえ、わずかな概念の集合しか既知の領域に移行していないとき低遷移と呼び、ある程度多くの概念の集合が既知の領域（Ｋ領域）に移行しているときに、高遷移と呼ぶことにしよう。

 

④全遷移

有限の概念の集合を考える場合、そのすべてが未知の領域から既知の領域に移行することはあり得る。

無限に多様な概念の集合の場合、まずすべてが未知の領域から既知の領域に移行する状況を考察することは非常に重要である。

しかし、現実の認識主体の立場からすると、そのすべてを既知の領域に遷移させる不可能だろう。

—————————————————————

 

事例；

 

意義

遷移度という概念の最大の意義は、未知の領域に属する無限に多様な概念の集合を考えることで、つねに自覚的に思考することができることである。

 

・・・

 

■概念の集合の分布

確言しておこう。

人類が獲得した偉大な理論は、かつてこのＵ領域に存在したものであり、来たるべき未来の哲学は、Ｕ領域から招来するものなのである。

 

明瞭度の概要

明瞭度とは、認識（領域）の状態および変遷を、光のイメージによって直感的に把握／表現するための概念である。

この概念は、認識領域を明るさ‐暗さという尺度・グラデーションによって捉える。

認識領域は、Ｋ領域／Ｕ領域に区分されるが、この境界線はファジーなものと考えられるため、明瞭度という尺度が重要になる。

 

明瞭度という尺度は、主として、認識（領域）の状態が概念の集合を通じてどのように変容したかを表現するために用いるものである。

ただし、補足で述べる通り、様々な使用方法があり、目的に応じて自由に使用できるものである。

 

※Ｋ領域／Ｕ領域の区分

※概念の機能論で述べた通り、概念の集合は、光学的な機能をもつ。

※補足：

明照度という方が正確かもしれない。

 

※補足：使用法の詳細

明瞭度という概念が前提としている認識とは、次のような様々な思考活動が関係するものである。

思考する・理解する・解釈する・解決する、気付く・分かる・思い付く…

またこの概念は、次のような認識の状態や構成要素を表現することができる。

認識の深さ／知識・情報量の多さ／理解度の高さ／視覚的なイメージの有無／言葉・語彙の豊富さ／言語化の度合い／記憶の鮮明さ…など様々なものを表現できる。

 

・・・

 

以下では、先ほどの遷移度の４つのパターン区分に従い、明瞭度の変化を考えてみよう。

明瞭度は、前述の遷移度と相互に影響を及ぼし合う関係性にあるためである。

—————————————————————

①無遷移➡無明照

第一のパターンは、

この場合、認識領域は、概念の集合を通じてまったく光によって照らされていない状態である。

 

②低遷移➡低明照

第二のパターンは、低明照の状態である。

 

③高遷移➡高明照

第三のパターンは、高明照の状態である。

 

④全遷移➡全明照

第四のパターンは、全明照の状態である。

—————————————————————

 

■遷移度と明瞭度

上記のパターン区分では、遷移度から明瞭度へというフローで確認した。

しかし、遷移度と明瞭度の関係性は、一方向的なものではなく、相互的なものである。

例えば、知覚情報を獲得することが、概念を獲得に繋がり、遷移度を高めるという関係も考えられる。

大量の知覚情報は、帰納的なパターン化を経て、新しい概念を獲得することに繋がる。

すると、新しい概念は、未知の領域から既知の領域へと地理学的にシフトし、遷移度が高めることになる。

 

■Ｋ領域／Ｕ領域

認識領域において、明瞭度が高い部分をライトエリア、明瞭度が低い部分をダークエリアと呼ぶことがある。

 

ライトエリア／ダークエリア

認識領域において、明瞭度が高い部分をライトエリア、明瞭度が低い部分をダークエリアと呼ぶことがある。

ライトエリア／ダークエリアという対概念は、Ｋ領域／Ｕ領域の区分に重なり合うが、前者は明瞭度に焦点を当てた表現であるのに対して、後者は認識の最も基本的な区分を重視した表現である。

 

■意義①認識を固定化しないこと

明瞭度という概念は、明るさ‐暗さという尺度・グラデーションの概念である。

明瞭度という概念の意義の一つは、

認識の状態とは変容し続ける可能性をもつものであり、つねに過渡的な変遷状態にあるものと解釈されることになることである。

 

■明瞭度のイメージ；油絵の創作過程

 

■明瞭度の事例イメージ；哲学書

 

——————————————————————-

■事例

明瞭度は、我々にとって極めて身近な認識の状態を表現する概念である。われわれは、毎日のように自身の認識領域の明瞭度を更新しているのである。
古代ギリシア時代の数学者・物理学者アルキメデスのエウレカ

プラトンの対話編『メノン』

教育現場、読書をするシーン
古代人とダークマター？

——————————————————————-

 

 

遷移度／明瞭度の機構（システム）

 

・遷移度と明瞭度の概念的な機構（システム）

次に、遷移度と明瞭度という概念の全体像を提示したい。

これまでの記述で、遷移度や明瞭度という尺度が、概念の集合と密接な関係があることが示された。

しかし、概念空間論のシステムにおいて、この対概念は

 

遷移度と明瞭度の機構

—————————————————————

①概念の集合

②遷移度、明瞭度

③問題解決度

—————————————————————

遷移度／明瞭度は、直感的であると同時に、極めて抽象度の高い概念である。

 

遷移度／明瞭度は、図式的あるいは構造的に理解される必要がある。

以下では、遷移度の仕組みを明確にするために、認識領域Ｒに加え、

平面上に平行に引かれた三本の線分を用いて話を進めたい。

 

—————————————————————

認識領域Ｒ：

第一の線分：概念量の線分

第二の線分：遷移度の線分、明瞭度の線分

第三の線分：問題解決状況の線分

—————————————————————

仮定１．すべての線分は平行に引かれている

これらの線分は、平面上に平行に引かれており、また各線分上では、固有の動点が滑らかに両極の間を移行していくものと仮定する。

結論から言えば、これらの動点は、（理想的な認識主体においては、条件が満たされていれば）基本的には相互に対応しながらつねに同じ方向にシフトしていく。

 

第一の線分は、概念量の線分Ｇｇである。

この線分は、概念の量の多寡、あるいは概念の充足度／不足度を表現する。

概念量線分の両端Ｇとｇは、この線分の極点である。

点Ｇは、概念の量が無限（∞）または最も多い状態を表し、点ｇは、概念の量がゼロ（０）または最も少ない状態を表す。

両極の間には、動点Ｑが存在する。

漸進的に、極点Ｇに近付くほど、概念の量は増加し概念の充足状態に近付き、極点ｇに近付くほど、概念の量は減少し、概念の不足状態に陥る。動点Ｑが極点ｇに一致する状態を、白紙状態（タブララサ）と呼べるだろう。

線分Ｇｇの中心には、中点Ｍ’がある。漸進的に、中点Ｍ’から極点Ｇまでの範囲は、概念の充足状態を表し、中点Ｍ’から極点ｇまでの範囲は、概念の不足状態を表すと考えられる。

 

第二の線分は、明瞭度の線分ＬＤである。

この線分は、明瞭度のグラデーションを表現している。

両端には、この線分における極点ＬとＤがある。

点Ｌは認識の明瞭度が最も高い状態を、点Ｄは明瞭度が最も低い状態を表す。

両極の間には、認識動点Ｒが存在する。

線分ＬＤの中心には、中点Ｍ（Ｌ）がある。中点Ｍから極点Ｌまでの範囲を、大まかにライトエリアと呼ぶ。反対に、中点Ｍから極点Ｄまでの範囲を、大まかにダークエリアと呼ぶ。

 

この線分ＬＤ上を、認識の状態を表現する動点Ｒが移動していくものとしよう。

動点Ｒの移行は、認識の変容およびそれに伴う明瞭度の変化を意味している。

 

第三の線分は、問題解決度の線分ＳＵである。

この線分は、問題解決の状況を表現する。

この線分の両端には、極点ＳとＵが存在する。

極点Ｓは、問題が完全に解決された状態、あるいは問題が消滅し存在しなくなる状態を表現する。

極点Ｕは、問題が解決不能な状態、あるいは問題が認識されず存在しなくなる状態を表現する。

両極の間には、同点Ｐが存在する。

点Ｓに近付くほど、問題は解決に近付き、あるいは問題が解決に至る可能性が高まると考えられる。

点Ｕに近付くほど、問題は解決困難な状態に陥るか、問題が解決不能な状態に至ると考えられる。

————————————————————–

 

以上で、明瞭度の機構を理解するための基本的なパーツは大方出揃ったことになる。

次に、各線分および動点同士の関係性を考察しよう。

※以下の考察では、理想的な認識主体を想定している。後述。

 

線分および動点同士の対応

 

以下のような流れを想定し、線分同士の対応を考察しよう。

※ただし、これは飽くまでも分かりやすい説明のため設定された順序であり、必ず１→４の流れで移行すると考える必要はない。

———————————————–

１．概念量線分上のシフト（動点Ｑの移動）

２．認識領域上の変化（Ｋ領域／Ｕ領域の変化）

３．明瞭度線分上の変化（動点Ｒの移動）

４．問題解決線分上の変化（動点Ｐの移動）

———————————————–

 

上記の線分は、相互に平行に引かれている。また認識領域＝Ｋ領域＋Ｕ領域と合わせて考えられる。

各線分上では、それぞれ動点が相互に対応してシフトしていく。

認識の変容は、自然に素朴に考えた場合、時間の推移のなかで起こる。

動点が動くきっかけは、概念量Ｑのシフトによる。

 

概念量の動点Ｑは、極点Ｇとｇの間を移行していく。

ここでは両極への移行を、正方向への移行、負方向への移行の２つのパターンに分けて描写する。

 

第一のパターン（正方向、増加方向へのシフト）

————————————————-

１．概念量線分上のシフト

概念量の線分Ｇｇにおいて、動点Ｑが極点Ｇに近付くにつれ、概念の量は増加していく。

 

２．認識領域上の変化

認識領域上では、Ｕ領域からＫ領域に、概念あるいは概念の集合が、シフトする。

あるいは概念の集合は、Ｋ領域およびＵ領域の特定の部分に光を当て、明瞭度の変化を引き起こす。

 

３．明瞭度線分上の変化

動点Ｇの正方向（＋）への運動、概念量の変化に伴い、

明瞭度線分上では、認識動点Ｒが極点Ｌに引き寄せられ、明瞭度が高まる。

４．問題解決線分上の変化

問題解決度の線分上では、動点Ｔが極点Ｓに移行し、問題解決の可能性もまた高まっていく。

————————————————-

 

※補足；極点Ｇ／Ｌ／Ｓについて

極点の解釈

極点Ｇは、概念量が無限に増加した状態を意味する。

動点Ｑが、完全に極点Ｇの位置に一致したとき、完全な充足状態に至る。

明瞭度線分➡解釈

明瞭度の線分は、認識の完全性を表現していると解釈できる。

明瞭度が最も高い状態とは、その問題や対象についての完全な認識がされる状態である。

極点Ｌにおいて、明瞭度は最も高い状態に至るが、その問題や対象についての完全な認識がされる状態である。

※極点Ｌは、理論的には、特定の物事について最も明瞭度が高い状態を表すが、実践的には、明瞭度の高まりには終わりがないため、極点Ｌに近付いていくことは可能だが、完全に到達することはない。

————————————————-

 

 

問題解決プロセス

——————————————————–

■問題解決の線分➡問題の発生／解決

明瞭度は、問題の発生および問題の解決に深く関係している。

まずは問題の発生について。

明瞭度が最も高い状態、すなわち点Ｌの位置では、いかなる問題も生じない。
明瞭度が最も低い状態、でも、いかなる問題も生じない。（古代人とダークマター）

ところが、

点Ｌあるいは点Ｄから少しでも明瞭度が変化すると、

認識主体にとって新しい問題が浮上するのである。

 

なぜなら、点Ｌに近い部分では、

まだ完全に光が当たっていない部位があるからであり、

点Ｄに近い部分では、完全に未知であった対象が姿を現し始め、

問題は、このようにＫ領域とＵ領域のファジーな境界線において生じるのである。

 

次に、問題の解決について。極点Ｌ

明瞭度が最も高い状態、すなわち点Ｌの位置では、あらゆる問題は解決に至っていることは明白である。

ただし、問題解決とは、必ずしも極点Ｌに至るまで明瞭度を高めなければならないとは限らない。

明瞭度線分上のある点において問題が発生したとき、