認識表現モデル（α稿）

第３章　認識表現モデル

————————————————

概念空間論と認識表現モデル

認識表現モデルとは、認識の状態および認識の変容を把握／表現するための図式である。

次の図は、全体像を表している。

■全体像

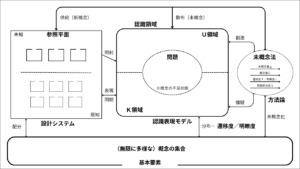
■認識表現モデルの構成要素

認識表現モデルには、次の概念が含まれる。

——————————————————————–

①Ｋ領域／Ｕ領域（認識領域Ｒ）

②遷移度／明瞭度

③概念関係式

——————————————————————–

①は、認識を空間的な範囲によって表現する概念である。

②は、認識領域Ｒの状態や変容を表現する尺度である。

③は、認識を複数の概念同士の結び付きによって表現するモデルである。

以下では、まず①～③の概念の概要、関係性や相違点を述べる。

・認識表現モデルの意義については、最後に述べる。

認識領域Ｒ

認識領域Ｒとは

認識領域Ｒとは、モナド的観点がもつ認識を空間的な範囲によって把握／表現する概念である。

記号としては、ＲまたはＥ（Ｒ）を使用することが多い。

認識領域の範囲；認識領域Ｒ＝Ｋ領域＋Ｕ領域

認識領域Ｒは、既知の領域（Ｋ領域）と未知の領域（Ｕ領域）に区分される。

逆に言えば、認識領域Ｒは、既知の領域（Ｋ領域）と未知の領域（Ｕ領域）を合わせた領域である。

そのため、両者の基本的な関係性は次の式で表現できる。

認識領域Ｒ＝Ｋ領域＋Ｕ領域

・Ｋ領域／Ｕ領域

Ｋ領域／Ｕ領域とは、認識主体にとっての認識（領域）を区分するための対概念である。

Ｋ領域（known area）とは、既知の領域を意味する。

Ｕ領域（Unknown area）とは、未知の領域を意味する。

ＫとＵの記号は英語のイニシャルに由来する。

ただし、「既知」「未知」という表現は主として「既に認識されている」「未だ認識されていない」という様々な認識を包括的に意味している。この表現は「既に知っている」「未だ知らない」というように、この表現から単純に喚起されるような、知識の状態という狭い意味で用いられている訳ではない。

・認識領域

Ｋ領域／Ｕ領域を合わせたものを、認識領域Ｒと呼ぶ。

両者は次のような関係性がある。認識領域＝Ｋ領域＋Ｕ領域

・認識領域Ｒ、Ｋ領域／Ｕ領域の構成要素

認識領域ＲおよびＫ領域／Ｕ領域には、認識を構成する様々な要素が含まれる。

構成要素の事例として、次のものが挙げられる。

概念の集合（概念）、個々の認識、知覚情報、知識、記憶、etc…

Ｋ領域とは、既存の認識――既知の概念の集合、知識、情報、考え方、信念など――が含まれる領域である。

Ｕ領域とは、未知の認識――未知の概念の集合、知識、情報、考え方、信念など――が含まれる領域である。

これらの構成要素は、認識領域Ｒ（＝Ｋ領域／Ｕ領域）上の適切な場所に配分され、移動することができる。

こうした考え方によって、認識の状態及び変容のプロセスを明確に記述することができるようになる。

・認識領域の設定；①認識主体／水準、②認識の種類

認識領域ＲおよびＫ領域／Ｕ領域という概念を用いる際は、２つの解釈パターンが考えられる。

——————————————————————–

１．抽象化され、純粋なモデルとして考えられるパターン

２．具体化され、認識水準／主体や認識の種類が設定され考えられるパターン

——————————————————————–

第一のパターンは、認識領域を純粋なモデルとして考えたものである。

第二のパターンは、認識領域を具体的なものとして解釈したものである。

認識領域ＲおよびＫ領域／Ｕ領域という概念には、具体的なものと考える場合、幾つかの設定項目がある。

——————————————————————–

①認識水準／認識主体

②認識の種類・切り口

——————————————————————–

第一の設定項目は、認識水準または認識主体である。

認識表現モデルは、様々な水準で用いることができる。

社会レベル、集団レベル、個人レベル、一般レベル、学問レベルなどである。

ここでは個人レベルを例に挙げよう。

Ｋ領域／Ｕ領域の状態は、各々の認識主体にとって固有のものである。当然ながら、認識主体が切り替われば、それに応じて認識領域の状態は全く異なるものになるだろう。各々の認識主体にとって、何が既知／未知であるかは異なる。

それゆえ、抽象化されたモデル的な観点を考えるケース以外は、具体的に「誰にとっての／どの水準における既知／未知なのか？」という点について明確にする必要がある。

第二の設定項目は、認識の種類または切り口である。

認識の水準や主体は、

認識領域は、様々な構成要素によって考えられる。

概念の集合、個々の認識、知覚、記憶などである。

■補足；

・Ｋ領域／Ｕ領域の注意点

ただし、この区分には幾つかの注意が必要である。

●ポイント１．Ｋ領域の主観性

Ｋ領域、あるいは既知とは、知識や認識の客観的な正しさを意味するものではない。

既知の領域とは、つねに特定の認識主体にとって既知であると信じられていることの領域なのである。

それゆえ、概念空間論では既知の領域を疑うための自覚的なシステムも組み込まれている。

設定項目の箇所で述べたが、特定の具体的な認識主体を設定した場合、それに応じて既知／未知の領域の状態や区分は変わる。

●ポイント２．認識領域の区分のファジー性

また認識の領域上に、既知／未知という明確な境界線を引くことが可能だと想定されている訳ではない。

認識領域およびその区分とは、図式的なモデルである。

●ポイント３．未知の領域のグラデーション

【K領域】についての重要な補足

Ｋ領域とは「既に認識されているもの」全体の領域のことなのですが、実はＫ領域の中にも「未だ認識されていないこと」が多く含まれています。既に知られている、既に理解している、既に見えている、、、というように「既知である、と考えられていること」の中には、実はそのように信じられているだけで、無数の「未だ認識されていないこと」が含まれているのですね。そのため、【Ｋ領域】について考えるうえで極めて重要なのは、「Ｋ領域の中にもＵ領域に属する新しい認識が含まれていないだろうか？」と疑う自覚的な思考、あるいは自覚的な認識となります。■【Ｋ領域】に含まれている「【Ｕ領域】に属する新しい認識」

【U領域】についての重要な補足

「Ｕ領域」には、定義上、私たちにとってのあらゆる「新しい認識」が含まれています。私たちが取り組むどんな問題についても、次のように想定することができます。「あらゆる問題についての「新しい認識」は必ず【Ｕ領域】に属している」これは、言い換えればこういうことを意味します。あらゆる問題解決シーンにおいて、答え（解）は、必ずＵ領域に存在するこのように想定することで、思考を促進する手立てが得られます。【Ｋ領域／Ｕ領域】という概念の最大の意義はここにあり、私がこの対概念を用いているのは、このような想定をするためです。

使用法

Ｋ領域／Ｕ領域という区分を用いると、認識を構成する様々な要素を配分し整理することができる。

まず①知覚情報、視覚的な【Ｋ領域／Ｕ領域】の事例を挙げよう。

ただし、持続的な時間の流れの中で刻一刻とＫ領域／Ｕ領域の内容は変遷していく。

■事例①目の前の景色自分の観点から見える、眼前の景色は「Ｋ領域」で、それ以外の自分の位置から見えないところは「Ｕ領域」に属する。

「Ｋ領域」➡自分の視界（目の前の景色）に含まれているもの。

「Ｕ領域」➡自分の視界に含まれていない、見えないもの。

■事例②書物の頁書物を繙くとき、開かれているページは「Ｋ領域」にあり、閉じられたページは「Ｕ領域」にあります。

■②【思考上のＫ領域／Ｕ領域】の事例

■事例①ミステリ小説の犯人

読み始めたばかりのミステリ小説の中で、「犯人が誰であるか」という認識は「Ｕ領域」にあり、小説を読み終える頃にはその認識は「Ｋ領域」に含まれることになる、と言えます。

■事例②学習のシーン

新しい分野の勉強をするシーンを考えてみます。この場合、既に知識があること・学んだこと・理解できたこと等は「Ｋ領域」に含まれ、未だ知識がない箇所・学んでいない事・理解できていないことは「Ｕ領域」に属します。

■事例③新しい天体

天文学者が新しい天体を発見し命名するとき、その天体に関する認識は「Ｕ領域」から「Ｋ領域」に移行することになる。

■事例④数学の問題の答え／未解決問題の解法

人類にとって、自数学の未解決問題の解を導く考え方は、人類にとって思考上の「Ｕ領域」に属すると考えられます。

・認識領域Ｒと概念の集合の関係

認識領域ＲおよびＫ領域／Ｕ領域は、概念の集合と次のような２種類／二重の関係性を持っている。

これらの関係性は、認識と概念の集合との関係性についての２つの解釈パターンである。

ただし、これらの解釈は、同じことを別の角度から表現したものでもある。

——————————————————————–

①地理学的な関係性（配分的、包含的な関係性）

②光学的な関係性

——————————————————————–

①地理学的な関係性（配分的関係、包含的関係）

第一の関係性は、地理学的な関係性である。

これは包含的関係、あるいは配分的関係と呼ぶこともできる。

この関係性において、次の２つの前提が置かれている。

——————————————————————–

１．概念の集合は、各々の認識の状態に応じて、Ｋ領域／Ｕ領域に配分される。

２．概念の集合は、認識の変容プロセスに応じて、Ｋ領域／Ｕ領域を移動する。

——————————————————————–

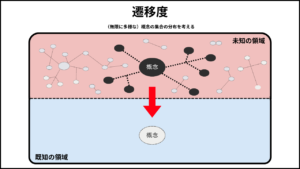
■参照平面

まず認識領域Ｒは、Ｋ領域／Ｕ領域に区分されるが、概念の集合はこの両領域の適切な部分に配分されることになる。換言すると、Ｋ領域／Ｕ領域は、それぞれ概念の集合を部分的に包含する。

概念空間論で扱う無限に多様な概念の集合は、基本的に、既知のグループと未知のグループに分類される。

これは無限に多様な概念の集合が、Ｋ領域／Ｕ領域に配分される、という意味である。

既知の概念のグループとは、Ｋ領域に配分・包含されたものであり、未知の概念のグループとは、Ｕ領域に配分・包含されたものである。

こうした分類方法によって、無限に多様な概念の集合は、扱いやすいものになるだろう。

■遷移度

さらに、認識領域Ｒと概念の集合の配分的／包含的な関係性は、静的なものではなく、認識の変容プロセスに応じて、刻一刻と変化しうる動的なものでもある。

認識領域とその構成要素の配置状態は、決して、永続的に同じ状態に留まる固定的なものではない。

この地理学的なシフトは、特定の操作や手続きによって意図的に起こるか、あるいは何らかの要因によって自然に起こると考えられる。

無限に多様な概念の集合のなかで、Ｕ領域（未知の領域）に属する概念のグループは、Ｋ領域（既知の領域）へとシフトしうるのである。また何らかの操作・手続き・要因によって、Ｋ領域（既知の領域）に属する概念のグループが、Ｕ領域（未知の領域）に移行させられることもあるだろう。

■未概念法、参照平面

概念空間論にとって、認識領域Ｒ（Ｋ領域／Ｕ領域）と概念の集合Ｇのこの地理学的な関係性は、極めて重要な意味をもつ。

まず、Ｕ領域に属する未知の概念のグループは、無限に多様な概念の集合Ｇによって集合論的に把捉されてはいるものの、そのままでは十分に使用することができない。そのため、何らかの方法を通じて、われわれはこれらの概念のグループを獲得しなければならないのである。

概念空間論では、未概念法という方法論によって、Ｕ領域に属する未知の概念のグループを、凄まじい速度でＫ領域にシフトさせる。換言すれば、Ｕ領域に属する無数の概念を、自由に思考することによって発見するのである。大陸のモチーフで表現するならば、これはＵ領域を自由に踏破するのである。この意味において、Ｕ領域に対して、われわれは勇敢（な冒険家）にならなければならない。

Ｋ領域に属する既知の概念のグループは、決してわれわれにとって完全な既知のものであると、つまり完全な認識が得られているものとは考えられない。

なぜなら、Ｋ領域に属する概念のグループは、ポジティヴな意味では、まだわれわれが認識できていないような新しい可能性を含むかもしれず、ネガティヴな意味では、何らかの思い込みやバイアスや誤りを含むかもしれないからである。

それゆえに、概念空間論では、様々な方策を通じてつねに「既知の概念のグループ」を疑う。

懐疑的な参照平面によって、あるいは未概念法によって、

未概念法では、既知の概念のグループを未概念として、すなわち過渡的な生成状態にある変容性の概念として見做すことによって、各々の概念がもちうる可能性のすべてを引き出す。また特定の思考モデルを構築する際には、殆どのケースにおいて、「思い込み集合」のようにそのパラダイムに対する懐疑的な概念を含めて思考を進める。

この意味において、Ｋ領域に属する概念のグループは、決してＫ領域の境界内部で安定的に存在するものではない。つねに、Ｕ領域との間で地理学的なシフトが生じうるのである。

思い込みを疑うこと、特定の認識主体にとって、想定されることはできても、そのままでは使用することができない。

ただし、この分類方法を採用する場合、次の点については注意が必要である。

Ｋ領域／Ｕ領域、すなわち既知の領域／未知の領域という区分は、単純な二分法を表しているわけではない。

前述のとおり、認識表現モデルには、明瞭度という概念が含まれている。

明瞭度とは、認識領域Ｒを明るい‐暗いという連続的なグラデーションで把握するための尺度である。

認識領域Ｒには、概念の集合をはじめとして、様々な構成要素が含まれるが、すべての構成要素にもまた、明瞭度という尺度が適用されると考えてほしい。

(無限に多様な)概念の集合は、Ｋ領域とＵ領域（既知の領域と未知の領域）に分配されるが、すべての概念について、明瞭度が考えられるのである。

ある概念または概念の集合が、Ｋ領域に属する場合でも、それが認識主体にとって完全に理解されているとは限らないし、かりに言葉では既知であると表現されるケースでも、思い込みやバイアスが完全に排されていることを保証するものではないのである。また、ある概念または概念の集合が、Ｕ領域に属する場合でも、そのまま完全なる未知を表現するとは限らない。もし、Ｕ領域に属する構成要素が、認識主体にとって、完全なる未知である（※明瞭度がゼロ）としたら、そもそもその存在すら全く認識されえないことになる。

認識表現モデルでは、Ｋ領域／Ｕ領域、既知／未知という区分は、つねに明瞭度というグラデーションによって把握される必要がある。

②光学的関係

第二の関係性は、光学的な関係性である。

概念の機能論で述べた通り、概念は光学的な機能をもち、認識領域Ｒを照らす効果がある。

光学的な関係性とは、概念の集合が、認識領域に光を照射し、明瞭度の変化を引き起こすという影響関係である。

無限に多様な概念の集合は、前述の包含的または配分的な関係において、Ｋ領域とＵ領域に分配された。

この配分方法は、光学的な関係性とパラレルなものであり、次のように読み替えることができる。

Ｋ領域（既知の領域）は、既存の概念のグループによって光を当てられた領域である。

Ｕ領域（未知の領域）は、未知の概念のグループによって光を当てられる領域である。

この光学的な関係性は、概念空間論という体系全体のイメージを掴むために、極めて重要である。

この体系内において、無限に多様な概念の集合を扱うのは、Ｕ領域とＫ領域の両領域を、すなわち認識領域Ｒ全体を余すところなく、膨大な光量によって照射するためだからである。

無限に多様な概念の集合とは、この光学的な関係性を通じて、認識領域の明瞭度を際限なく高めるためのものである。