未曲項散布➔遷移度
: 2023年9月12日
こんにちは、馬渕です。
このページでは、転覆地図論におけるテキスタイルという概念についてご紹介します。
※開発中で未完成の概念です。
※記事は追記・修正中です。
転覆地図論とテキスタイル
現在、転覆地図論という新しい理論・方法論の開発に取り組んでいます。
概念空間論は既に完成しているのですが、転覆地図論はまだ完成していません。
概念空間論は概念の集合を扱う体系なのですが、
転覆地図論は曲線の集合を扱う体系になります。
転覆地図論は、イメージとしては概念空間論をトポロジー的に進化・深化させてさらに拡張した強力な考え方・方法論になると思います。
転覆とは大きな認識の変化のことです。
例えば、「世界観が変わる」ような体験を誰もが経験したことがあると思います。
私は、こうした転覆=認識の変化には、曲線の集合=テキスタイルというものが深く関係していると考えています。
転覆地図とは、大きな認識の変化を引き起こすように設計された曲線の集合=テキスタイルのことです。
転覆地図とは、曲線の集合=テキスタイルを通じて、大きな認識の変化を引き起こすための理論・方法論になります。
テキスタイル
テキスタイル(textile)とは、一般的に織物・布地のことを指します。
転覆地図論においては、テキスタイルとは主として曲線の集合体のことを意味します。
現在のところ、次のような意味規定を考えています。(未完成!)
①関係性の曲線
③可能性の曲線
④知覚の曲線/介在・伝達の曲線/行動の曲線
■テキスタイル・モデル
テキスタイルは、無限に多様な折り畳みや展開ができる折り紙・織物・布地のようなもの
テキスタイルは、概念の集合、曲線の集合、振動の集合などによって構成される
テキスタイルは、未曲線、実線体/虚線体の運動によって導かれ構造が決まる。
テキスタイルは、つねに生成・構成され続けるダイナミズムを持つ
テキスタイルは、基本的な有限個のパラメータを持つと仮定(※パラメータの具体的な特定は未完成)
テキスタイルは、パラメータの変動によって、あらゆる最も基礎的な概念や曲線を記述・生成可能と想定
(※具体的なパラメータ値のグループをテキスタイル・データと呼ぶ)
テキスタイルは、襞演算pli(⇄重折/開展)の操作ができる
テキスタイルは、次元をもつ
テキスタイルは、層構造(複数のテキスタイルの組み合わせ、重ね合わせ)をもつと想定。
テキスタイルには、必要な場合は多軸体を想定(時間軸、抽象度軸(情報量)など)
※1.テキスタイルの変形(折り畳みや展開)による襞・折り目が曲線になる、あるいは曲線と見做される。
※2.基礎概念/曲線/振動は、その組み合わせによってあらゆる複雑・応用・発展的な曲線/概念/振動を分解・再構成できる。
■テキスタイル種類➡転覆の事例
①学問的テキスタイル
哲学:哲学思想➡哲学的な思索や理解の過程で起こる世界観の変化
認知科学:個人の意識、思考、認識および固定的な思い込みや信念体系やパラダイムなど(認知テキスタイル)
数学:方程式、グラフ(量的、数値的テキスタイル)など。
芸術:美しい絵画、彫刻、建築➡鑑賞による感動など
経済・金融:為替や株価変動、チャートの集合(マクロ指標、株価など)➡株価の大暴落による世界の混乱、投資家のパニックなど(※需要・供給/期待/貨幣量/外部要因→物価上昇→政策金利引上げ→通貨高)
解剖学:身体全体の状態(健康、病気を含む)、毛髪、骨格系、血管系、栄養・ホルモン経路など
精神医学:精神疾患(うつ病、双極性障害など)、依存症など
論理学:命題(逆、裏、対偶(彼女がアリスならば、彼女はウサギの穴に落ちる。対偶:彼女がウサギの穴に落ちないならば、彼女はアリスではない))
宗教学:信仰
日常的:色々➡大きな事件・事故による驚き、パニック、センセーショナルなど
時間:時間による思考・感情への影響、時刻による意思決定の変化
空間:物質的なテキスタイル
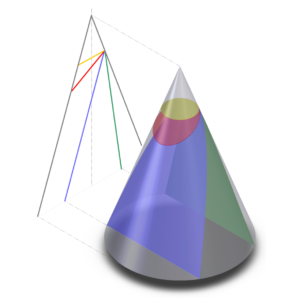
ーーーーーーーーーーー
曲線の分類
暗曲線/明曲線
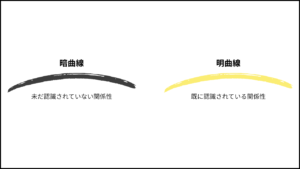
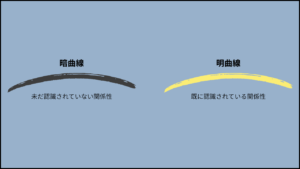
以下は、雑多なメモなのでスルーしてくださいm(__)m
↓ ↓ ↓
問題に対する曲線
モチーフ;曲線
■分岐系
分岐点、
分岐回数、
分岐階層
多重分岐
分岐種、順番分岐、場合分岐、
持続線、記号系列帯
問題P=””
参照面▭={}
問いQ=?___
Uarea={}
condi()={}
分岐Y
Th(X)=Φ,erroe,
参照面▭
Q=?___
思考方法のモチーフ
これから解説する思考方法は、光学・幾何学・裁縫あるいは織物仕事をモチーフとしている。
新しい概念を
概要
思考のモチーフ
【参照面】
【概念の不足状態】
【U領域】
【テキスタイル】
【襞】の操作、重折記号(Pli→)
折り方の集合・分類→関係性
【虚線体】
【i−テキスタイル】
【参照面】
参照面を構成する無数の観点は、各々の固有の観点から世界をあるいは対象を照らし出す。固有の切り口で捉える。
【参照面】の課題
【参照面】の概念は、【概念の不足状態】を前提としている。したがって、新しい観点を供給するルートないしシステムが必要になる。
【テキスタイル】(Textile)
ここで新しい概念を導入しよう。
【テキスタイル】とは、観点ないし概念の素材になる、布地のことである。
【テキスタイル】
■【テキスタイル(textile)】
イメージ:折り紙
特性:無限に折り畳まれる(襞の操作 pli→)
備考:テキスタイルは、無限に折り畳まれることで、観点あるいは概念となり、【参照面】に新しい観点や概念として加えられることになる。
布地(Textile)が
われわれが折り畳むことができる
【テキスタイル】(Textile)
思考の方法論上の課題
観点ないしそれを媒介する概念は、テキスタイル(布地)を素材とし、それを折り畳むことによって生じる。
無限に折り畳まれることによって、テキスタイルは他と区別されるような特異的な折り目(テキスチャー)を獲得し、観点は固有のものとなる。
ここまでの考察によって、思考の方法論上の課題とは、【テキスタイル】の折り方にあることが判明した。新しい観点ないし概念を生み出し、物事に対する新たな切り口を齎すのは
折ることと関係性
なぜ、事物は常に関係をもつのか。
【襞】の操作と記号
今我々の眼前に一つのテキスタイル、つまり一枚の布地が置かれている。
【テキスタイル】に対してできることは、折り畳むことである。そこで、手の平で無作為に折り畳む
すると、この布地に刻まれた無数の折り目は、固有の折り目の組み合わせ、曲線の集合を形作っている。(テキスチャー)
ここで、一枚の折り紙を折り畳むことが、容易く無限に至ることを思い起こして頂きたい。
テキスタイルを折り畳むこの操作を、襞と呼び、記号としておこう。
微分・解析学における極限の記号(lim)がある変数を限りなく特定の値に近付けることを意味する。これと同様に、襞の記号(Pli→)は、テキスタイルを無限に折り畳むことを意味する。無限に至る襞、折り目の配列が特異的なものになったとき、収束するものと考えよう。
テキスタイルは、幾つかの概念から構成されている。ここで重要なのは、幾つかの概念だけを扱う場合でも、襞の操作によって、すなわち折り畳むことによって、新しい折り目の配列に対応する新しい観点が生成する、これは一つの概念の誕生の瞬間でもある。
こうして折り畳まれた一つのテキスタイルと、一つの観点、一つの概念が生成する。
この観点を、新しく【参照面】に加える訳だ。
折り方について
テキスタイルを無限に折り畳むことによって、観点あるいは概念が生じる。これが意味するのは、新しい観点を生み出すことができるか否かは、「新しい折り方」を開発することに懸かっている。テキスタイルの新しい折り畳み方。
テキスタイルの新しい折り方の手掛かりを探るために、まず既存の折り畳み方を検討しよう。
折ることとは何か
物事を接続し関係性を持たせること、二重化すること。
折り方の種類・パターン
量的な折り方・バランス
分岐・
反射・反映・リフレクション
【虚線体】
【虚線体】i−Factor
1.観点から逃れ去る
2.関係性の否定、崩壊
3.指示ベクトルの
4.述語【虚線体】のふるまい
集合上、論理上、平面上、図形上
【虚線体関係式】(例)「ここにペンがある」



コメント