絡み合う曲線なしに、直線はありえない
――― G.W.ライプニッツ ――
このページでは、【曲線】についての研究をまとめていく。
【問題】研究テーマ
この世界が、こんなにも多くの曲線に満ちているのはなぜだろうか?
曲線的な世界への疑問
曲線の語義
curve, line
例えば、物理学のパースペクティヴから考えられる。
物理的には「波」であるものは、幾何学的には「曲線」として考えられるだろう。
では、あらゆるものが物理的に振動するからこそ、我々の目に映る世界も「曲線」が多いのだろうか?
それとも、目に映る世界が曲線に満ちているのは、もっと他に深遠な意味があるのだろうか?
襞-曲線の哲学
曲線の用語集
曲率
曲線には曲率という「線の曲がり具合」を表す概念がある。
ある曲線の「曲率が0」である場合、それは直線と見做される。
つまり、直線とは曲線の特殊なケースであり、一つのパターンに過ぎない。
曲線の分類
ニュートンによる分類
ニュートンは曲線を代数曲線と超越曲線の二つに分類した。
代数曲線
代数方程式で表示できる曲線。
例えば、単位円は多項式 x2 + y2 − 1 の零点集合となる代数曲線である。
超越曲線
非代数的曲線。積極的な意味を持たず、代数的ではない曲線のこと。
(例)正弦曲線や余弦曲線、対数曲線、サイクロイドなど。
曲線の種類
円錐曲線
二次曲線
円
楕円
放物線
双曲線
高次曲線
3次曲線
4次曲線
高次曲線
-アステロイド
-円系コンコイド
特殊な曲線系
螺旋形
アルキメデスの渦巻線(正渦線)
対数螺旋(等角螺旋)
周転曲線
サイクロイド(点Pが円周上)
トロコイド(点Pが円周の内か外)
エピサイクロイド(外サイクロイド)
カージオイド(心臓形)
ハイポサイクロイド(内サイクロイド)
アステロイド(星芒形)
リマソン(パスカルの蝸牛形)
その他の曲線
リサージュ曲線
インボリュート曲線
正葉曲線(バラ曲線)
レムニスケート(連珠形)
ペアノ曲線
漸近線曲線
シッソイド(疾走線)
トラクトリックス(牽引線)
ストロフォイド(葉形線)
コンコイド(ニコメデスの)
曲線の歴史
円錐曲線の歴史
古代ギリシアでは円錐の切り口として、後に
アポロニウスによって
曲線の種類・分類

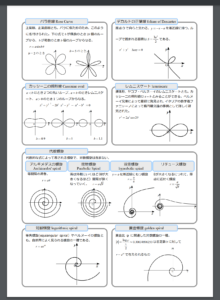

資料・参考文献
『曲線の事典』
『襞』ジル・ドゥルーズ
『深遠なる幾何学の世界』
ヒース
Lockwood, E. H (1961). A Book of Curves. Cambridge
微積分SP‐フェーズⅠ
微積分SP‐フェーズⅡ
微積分SP‐フェーズⅢ
数学の歴史
2020年11月-11月 ■古代の数学 ●古代オリエント -メソポタミア -エジプト -古代中国 ●古代ギリシア -ヘレニズム時代 -古代末期 -東地中海 ■中世の数学 ●古典期イスラーム世界 ●中世ヨーロッパ ■近世ヨーロッパ ●17世紀科学革命・近代数学の始原 ●18世紀ヨーロッパ ■近代数学の展開 ●第二の科学革命と解析革命 ●東アジアの近代西洋数学の需要 ●20世紀数学の思想 ■
■決定論 もしある瞬間における世界の状態(初期状態)に関する情報が完全に分かれば、全ての自然現象は完全に予知できるとする哲学的な原理のこと。
微積分の哲学的な研究
微分積分の歴史
微分が誕生したのは、12世紀。
インドのバースカラ2世
積分は、紀元前1800年頃。
アルキメデスの求積法。
微積分の基本定理
微分と積分は互いに独立に誕生したが、ニュートンとライプニッツがそれを結び付けた。
積分は微分の逆演算である、として。
微分の年表
ルネ・デカルト1596~1650 ピエール・ド・フェルマ1601~1665 アイザック・バロウ(Barow)1630~1677 アイザック・ニュートン1642 ~1727 ゴットフリート・ヴィルヘルム・ライプニッツ1646~1716 ベルヌーイ兄弟 ヤコブ1654~ 1705 , ヨハン1667~1748, レオンハルト・オイラー(1703~1783) ジョセフ・ルイ・ラグランジュ(1736~1813) オーギュスタン=ルイ・コーシー(1789~1857)
ライプニッツの微分 微分計算の過程は、小さい区間上で関数を、その関数の微分、すなわち接線の一部分で置き換えること。置き換えが行われる区間を、無限小と呼ぶ。微分計算とは、関数を無限少量に分解すること。
・微分積分の歴史
・アルキメデスの取り尽くし法・ニュートンの章・流率、微分・ライプニッツの微分・ライプニッツの記号法・無限小、微分、モナド・極限概念の導入 数学講座 【数学講座】概要 ■四則演算■数学分野代数学幾何学解析学数の体系数の基礎付け関係性、数学における
積分



コメント